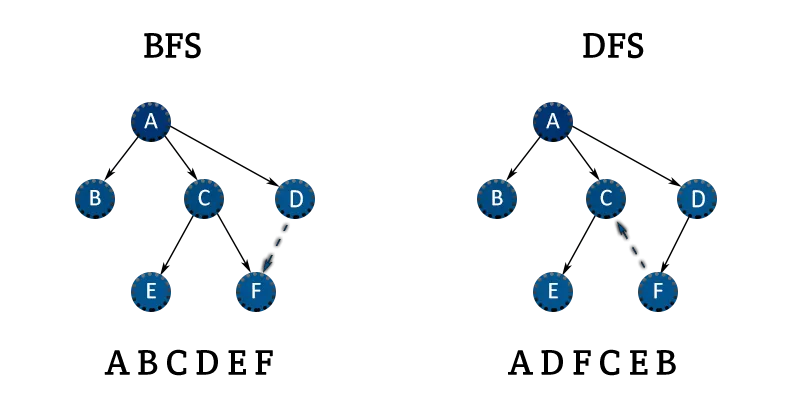
그래프 탐색
•
개념 : 어떤것들이 연속해서 이어질때, 모두 확인하는 방법
•
Graph : Vertex(어떤것) + Edge(이어지는 것)
그래프 탐색의 종류
1.
BFS: Breadth-first search (너비 우선 탐색)
2.
DFS: Depth-first search (깊이 우선 탐색)
BFS
아이디어
•
시작점에 연결된 Vertex 찾기
•
찾은 Vertex를 Queue에 저장
•
Queue의 가장 먼저 것을 뽑아서 반복
시간복잡도 : O(V + E)
BFS에 필요한 자료구조
•
검색할 그래프 (board, map 등…)
•
방문여부 확인 (재방문 금지해야하기 때문)
•
Queue (BFS를 실행할 큐)
String[][] map = new String[n][m];
boolean[][] visited = new boolean[n][m];
Queue<int[]> queue = new LinkedList<>();
int[] dx = new int[]{-1, 1, 0, 0,};
int[] dy = new int[]{0, 0, -1, 1};
// queue가 비어있을 때까지 탐색
while(!queue.isEmpty()) {
// 탐색
for(int i = 0; i < 4; ++i) {
// 조건을 만족시킬 경우 (도착지점에 도착한 경우 등)
return count;
// dx, dy를 더하며 탐색
// 조건을 만족하면 dx, dy를 더한다.
// 방문 [x + dx[i]][y + dy[i]] true로 업데이트
// dfs(nx, ny, ++count); 이런식으로 호출
}
// 조건을 만족시키지 못할 경우
// -1
}
Java
복사
DFS
그래프 탐색은 대부분 BFS로 처리가 가능하다.
DFS는 재귀함수를 사용하고 이는 백트래킹으로 이어진다.
•
주의할 점
◦
재귀 함수가 종료되는 시점을 반드시 명시
▪
안하면 무한 루프
◦
재귀함수의 깊이가 너무 깊어지면 Stack Overflow 발생
•
아이디어
◦
시작점에 연결된 Vertex 찾기
◦
연결된 Vertex를 끝날 때까지 찾음
◦
더 이상 연결된 Vertex가 없는 경우 다음 노드를 검색
시간복잡도 : O(V + E)
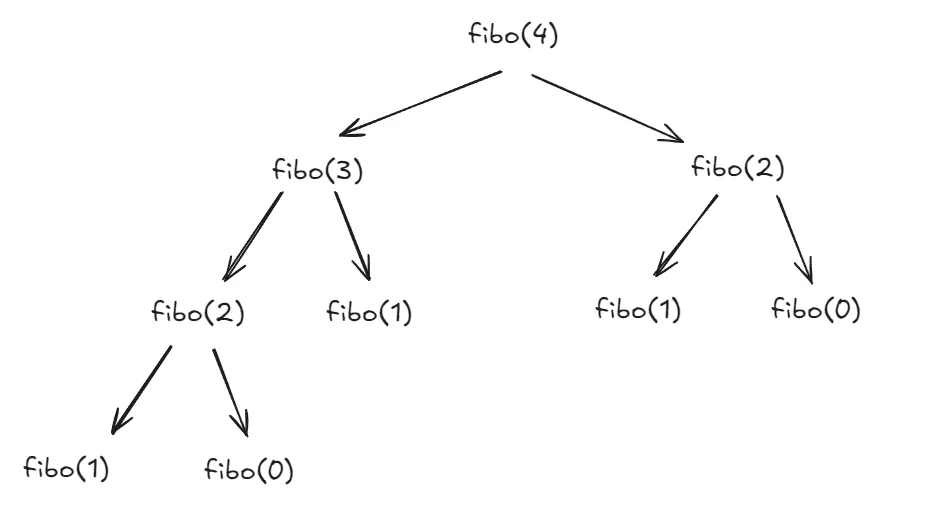
fun fibo(int n) {
// 기저사례 (재귀를 종료하는 조건)
if(n == 0 || n == 1)
return n;
return fibo(n-1) + fibo(n-2);
}
Kotlin
복사